1560. 圆形赛道上经过次数最多的扇区

🟢 🔖 数组 模拟 🔗 力扣open in new window LeetCodeopen in new window

题目

Given an integer n and an integer array rounds. We have a circular track which consists of n sectors labeled from 1 to n. A marathon will be held on this track, the marathon consists of m rounds. The ith round starts at sector rounds[i - 1] and ends at sector rounds[i]. For example, round 1 starts at sector rounds[0] and ends at sector rounds[1]

Return an array of the most visited sectors sorted in ascending order.

Notice that you circulate the track in ascending order of sector numbers in the counter-clockwise direction (See the first example).

Example 1:

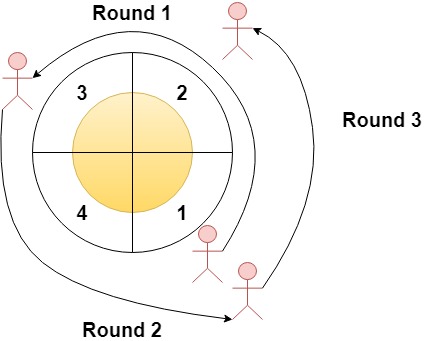
Input: n = 4, rounds = [1,3,1,2]
Output: [1,2]
Explanation: The marathon starts at sector 1. The order of the visited sectors is as follows:
1 --> 2 --> 3 (end of round 1) --> 4 --> 1 (end of round 2) --> 2 (end of round 3 and the marathon)
We can see that both sectors 1 and 2 are visited twice and they are the most visited sectors. Sectors 3 and 4 are visited only once.

Example 2:

Input: n = 2, rounds = [2,1,2,1,2,1,2,1,2]
Output: [2]

Example 3:

Input: n = 7, rounds = [1,3,5,7]
Output: [1,2,3,4,5,6,7]

Constraints:

2 <= n <= 100
1 <= m <= 100
rounds.length == m + 1
1 <= rounds[i] <= n
rounds[i] != rounds[i + 1] for 0 <= i < m

题目大意

给你一个整数 n 和一个整数数组 rounds 。有一条圆形赛道由 n 个扇区组成，扇区编号从 1 到 n 。现将在这条赛道上举办一场马拉松比赛，该马拉松全程由 m 个阶段组成。其中，第 i 个阶段将会从扇区 rounds[i - 1] 开始，到扇区 rounds[i] 结束。举例来说，第 1 阶段从 rounds[0] 开始，到 rounds[1] 结束。

请你以数组形式返回经过次数最多的那几个扇区，按扇区编号升序排列。

注意，赛道按扇区编号升序逆时针形成一个圆（请参见第一个示例）。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc- upload/uploads/2020/08/22/3rd45e.jpg)

输入： n = 4, rounds = [1,3,1,2]
输出：[1,2]
解释： 本场马拉松比赛从扇区 1 开始。经过各个扇区的次序如下所示：
1 --> 2 --> 3（阶段 1 结束）--> 4 --> 1（阶段 2 结束）--> 2（阶段 3 结束，即本场马拉松结束）
其中，扇区 1 和 2 都经过了两次，它们是经过次数最多的两个扇区。扇区 3 和 4 都只经过了一次。

示例 2：

输入： n = 2, rounds = [2,1,2,1,2,1,2,1,2]
输出：[2]

示例 3：

输入： n = 7, rounds = [1,3,5,7]
输出：[1,2,3,4,5,6,7]

提示：

2 <= n <= 100
1 <= m <= 100
rounds.length == m + 1
1 <= rounds[i] <= n
rounds[i] != rounds[i + 1] ，其中 0 <= i < m

解题思路

由于赛道按扇区编号升序形成一个圆，所以我们只需要关注起点和终点，分为以下三种情况：

start == end
- 如果开始和结束在同一扇区，可以看出，起点比其他扇区多一次访问。
- 因此，访问最多的点就是起点 start。
```
            s---------- n
1 --------------------- n
1 --------------------- n
1 --------- e
```

start < end
- 如果开始扇区在结束扇区之前，可以看出，起点和终点之间的扇区比其他扇区多一次访问。
- 因此，访问最多的点就是 [start, end]。
```
      s -------------- n
1 --------------------- n
1 --------------------- n
1 --------------- e
```

start > end
- 如果开始扇区在结束扇区之后，可以看出，访问最多的扇区分为两个部分，分别是：
  - 从起点 start 到赛道的末尾 n 之间的扇区（[start, n]）；
  - 从赛道的起始位置 1 到终点 end 之间的扇区（[1, end]）；
- 因此，访问最多的点就是 [start, n] + [1, end]。
```
                s ----- n
1 --------------------- n
1 --------------------- n
1 ----- e
```

具体实现：

定义变量：
- 定义变量 start = rounds[0] 代表起始扇区；
- 定义变量 end = rounds[rounds.length - 1] 代表终点扇区；
- rounds 是比赛经过的扇区顺序，rounds[0] 是起始扇区，rounds[rounds.length - 1] 是终点扇区。
定义一个辅助函数 buildArr(a, b)，用于生成 [a, a+1, ..., b] 的连续数组，简化代码逻辑。
根据起点和终点的关系，选择不同方式生成结果数组。
- 如果 start == end，直接返回 [start]。
- 如果 start < end，返回从 start 到 end 的连续数组。
- 如果 start < end，返回从 1 到 end 的连续数组，加上从 start 到 n 的连续数组。

复杂度分析

时间复杂度：O(n)
- 辅助函数 buildArr(a, b) 的复杂度是 O(k)，其中 k 是生成连续数组的长度，k = b - a + 1。
- 最坏情况下，需要生成长度为 n 的连续数组，因此时间复杂度是 O(n)。
空间复杂度：O(n)，结果数组所占的空间。

代码

/**
 * @param {number} n
 * @param {number[]} rounds
 * @return {number[]}
 */
var mostVisited = function (n, rounds) {
	const m = rounds.length - 1;
	let res = [];
	const start = rounds[0];
	const end = rounds[m];

	const buildArr = (a, b) => new Array(b - a + 1).fill(a).map((a, i) => a + i);

	if (start == end) return [start];
	if (start < end) return buildArr(start, end);
	return buildArr(1, end).concat(buildArr(start, n));
};

1560. 圆形赛道上经过次数最多的扇区

# 1560. 圆形赛道上经过次数最多的扇区

# 题目

# 题目大意

# 解题思路

# 复杂度分析

# 代码

1560. 圆形赛道上经过次数最多的扇区

题目

题目大意

解题思路

复杂度分析

代码