986. 区间列表的交集

🟠   🔖  数组 双指针  🔗 力扣 LeetCode

题目

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

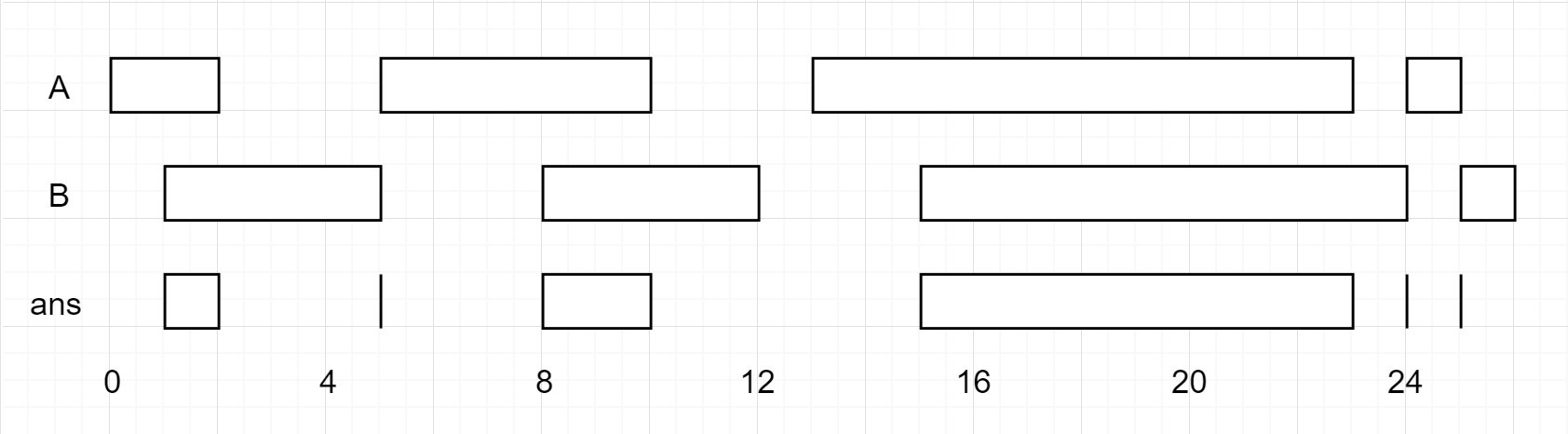
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]

Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []

Output: []

Constraints:

• 0 <= firstList.length, secondList.length <= 1000
• firstList.length + secondList.length >= 1
• 0 <= starti < endi <= 10^9
• endi < starti+1
• 0 <= startj < endj <= 10^9
• endj < startj+1

题目大意

给定两个由一些 闭区间 组成的列表，firstList 和 secondList ，其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。每个区间列表都是成对 不相交 的，并且 已经排序 。

返回这 两个区间列表的交集 。

形式上，闭区间 [a, b]（其中 a <= b）表示实数 x 的集合，而 a <= x <= b 。

两个闭区间的 交集 是一组实数，要么为空集，要么为闭区间。例如，[1, 3] 和 [2, 4] 的交集为 [2, 3] 。

解题思路

我们用 [a1, a2] 和 [b1, b2] 表示在 A 和 B 中的两个区间，如果这两个区间有交集，需满足 b2 >= a1 && a2 >= b1，分下面四种情况：

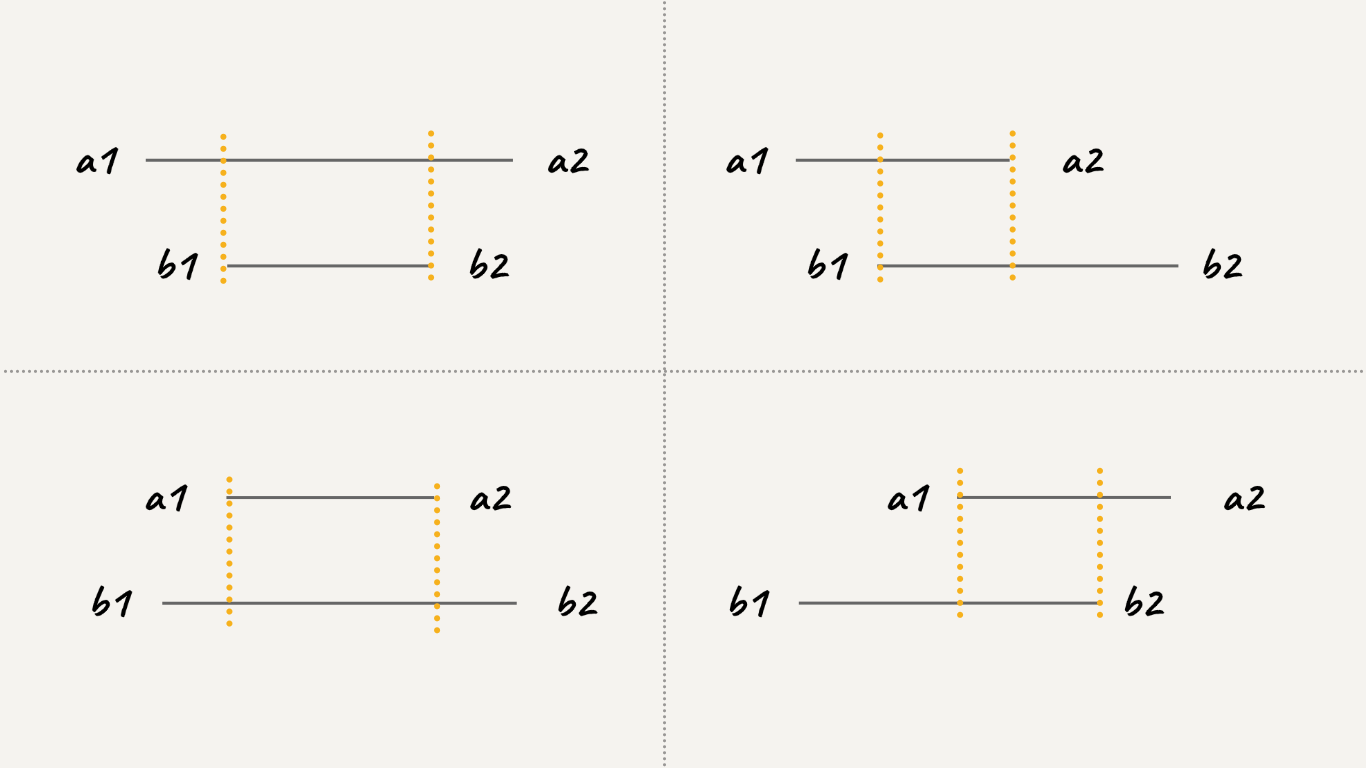
根据上图可以发现规律，假设交集区间是 [c1, c2]，那么

• c1 = max(a1, b1)
• c2 = min(a2, b2)

这一点就是寻找交集的核心。

代码

/**
 * @param {number[][]} firstList
 * @param {number[][]} secondList
 * @return {number[][]}
 */
var intervalIntersection = function (firstList, secondList) {
	let res = [],
		i = 0,
		j = 0;
	while (i < firstList.length && j < secondList.length) {
		let a1 = firstList[i][0],
			a2 = firstList[i][1],
			b1 = secondList[j][0],
			b2 = secondList[j][1];
		if (a1 <= b2 && a2 >= b1) {
			res.push([Math.max(a1, b1), Math.min(a2, b2)]);
		}
		if (b2 < a2) {
			j++;
		} else {
			i++;
		}
	}
	return res;
};

相关题目

题号	标题	题解	标签	难度	力扣
56	合并区间	[✓]	数组 排序	🟠	🀄️ 🔗
88	合并两个有序数组	[✓]	数组 双指针 排序	🟢	🀄️ 🔗
759	员工空闲时间 🔒		数组 排序 堆（优先队列）	🔴	🀄️ 🔗
2410	运动员和训练师的最大匹配数		贪心 数组 双指针 1+	🟠	🀄️ 🔗