938. 二叉搜索树的范围和

🟢   🔖  树 深度优先搜索 二叉搜索树 二叉树  🔗 力扣 LeetCode

题目

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range[low, high].

Example 1:

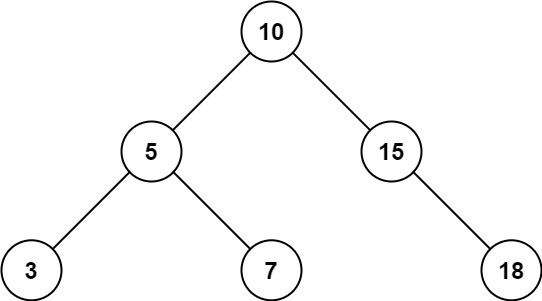
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15

Output: 32

Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

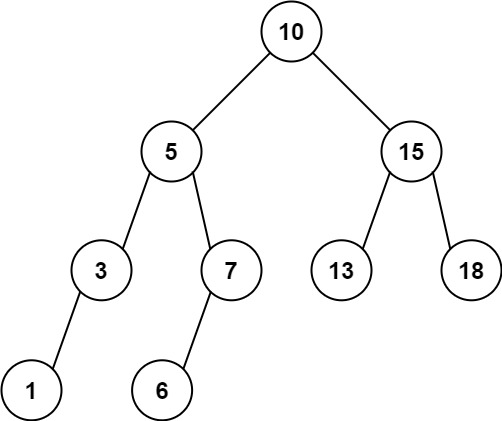
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10

Output: 23

Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints:

• The number of nodes in the tree is in the range [1, 2 * 104].
• 1 <= Node.val <= 10^5
• 1 <= low <= high <= 10^5
• All Node.val are unique.

题目大意

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入： root = [10,5,15,3,7,null,18], low = 7, high = 15

输出： 32

示例 2：

输入： root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10

输出： 23

提示：

• 树中节点数目在范围 [1, 2 * 104] 内
• 1 <= Node.val <= 10^5
• 1 <= low <= high <= 10^5
• 所有 Node.val 互不相同

解题思路

题目要求我们计算二叉搜索树（BST）中所有值在 low 和 high 范围内的节点值的和。利用二叉搜索树的性质，可以优化搜索过程。

1. 二叉搜索树的性质：

   • 对于任意节点 root，如果 root.val 小于 low，那么其左子树的所有节点值都小于 root.val，因此不需要再遍历左子树。
   • 如果 root.val 大于 high，那么其右子树的所有节点值都大于 root.val，因此不需要再遍历右子树。
   • 如果 root.val 在 [low, high] 范围内，则将其值加到总和中，并继续遍历左右子树。

2. 递归策略：

   • 从根节点开始，递归遍历二叉搜索树。
   • 在每个节点上判断其值是否在 low 和 high 范围内，如果是，则将其值加到 sum 中。
   • 递归左子树时，只在当前节点的值大于等于 low 时进行。
   • 递归右子树时，只在当前节点的值小于等于 high 时进行。

3. 边界情况：

   • 如果树为空，返回 0。
   • 如果所有节点的值都在范围外，则返回 0。

复杂度分析

• 时间复杂度: O(n)，其中 n 是树中节点的数量。最坏情况下，我们需要遍历整棵树。
• 空间复杂度: O(h)，其中 h 是树的高度。递归调用栈的最大深度为树的高度，最坏情况下是 O(n)，即树为链状时。

代码

/**
 * @param {TreeNode} root
 * @param {number} low
 * @param {number} high
 * @return {number}
 */
var rangeSumBST = function (root, low, high) {
	let sum = 0;

	const dfs = (node) => {
		if (!node) return;

		if (node.val >= low && node.val <= high) {
			sum += node.val;
		}

		// 如果当前节点值大于等于low，则可以继续遍历左子树
		if (node.val >= low) {
			dfs(node.left);
		}

		// 如果当前节点值小于等于high，则可以继续遍历右子树
		if (node.val <= high) {
			dfs(node.right);
		}
	};

	dfs(root);

	return sum;
};