931. 下降路径最小和

🟠   🔖  数组 动态规划 矩阵  🔗 力扣 LeetCode

题目

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

Example 1:

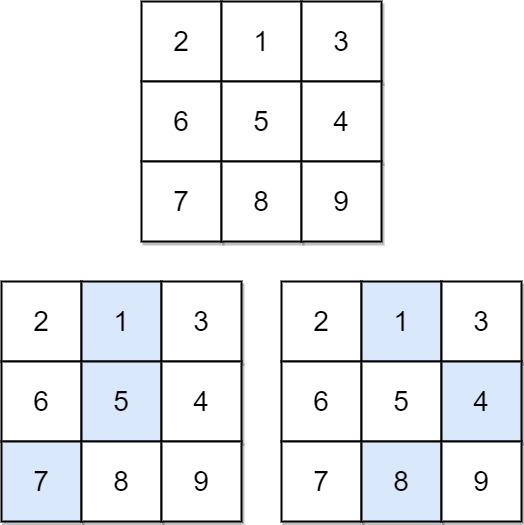
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]

Output: 13

Explanation: There are two falling paths with a minimum sum as shown.

Example 2:

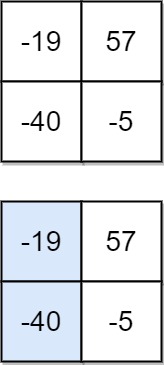
Input: matrix = [[-19,57],[-40,-5]]

Output: -59

Explanation: The falling path with a minimum sum is shown.

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

题目大意

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的 下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

解题思路

这是一个典型的动态规划问题。可以采用自底向上的方法，从矩阵的倒数第二行开始，逐行更新，直到第一行。

定义状态 dp[i][j] 为从第一行（matrix[0][..]）向下落，落到位置 matrix[i][j] 的最小路径和为 dp[i][j]。那么，dp[i][j] 的值可以通过考虑从 dp[i-1][j-1]，dp[i-1][j] 和 dp[i-1][j+1] 这三个路径和中，选择其中路径和最小的一个。

具体的状态转移方程为：

dp[i][j] = matrix[i][j] + Math.min(dp[i - 1][j - 1], dp[i - 1][j], dp[i - 1][j + 1])

最终，我们只需从 dp 数组的最后一行中找到最小的路径和，即为最终的答案：

return Math.min(...dp[m - 1]);

由于 dp[i][j] 只和 dp[i - 1][...] 有关，所以可以进一步优化空间复杂度，除了可以将 dp 数组降维以外，甚至可以不使用 dp 数组，直接原地修改 matrix 数组。

复杂度分析

• 时间复杂度：O(m * n)，其中 m 为矩阵行数，n 为矩阵列数，需要遍历整个矩阵。
• 空间复杂度：O(1)，原地修改矩阵。

代码

/**
 * @param {number[][]} matrix
 * @return {number}
 */
var minFallingPathSum = function (matrix) {
	const m = matrix.length;
	const n = matrix[0].length;

	// 从倒数第二行开始逐行更新
	for (let i = 1; i < m; i++) {
		for (let j = 0; j < n; j++) {
			// 考虑边界情况
			if (j == 0) {
				matrix[i][j] =
					Math.min(matrix[i - 1][j], matrix[i - 1][j + 1]) + matrix[i][j];
			} else if (j == n - 1) {
				matrix[i][j] =
					Math.min(matrix[i - 1][j - 1], matrix[i - 1][j]) + matrix[i][j];
			} else {
				matrix[i][j] =
					Math.min(
						matrix[i - 1][j - 1],
						matrix[i - 1][j],
						matrix[i - 1][j + 1]
					) + matrix[i][j];
			}
		}
	}
	// 返回最后一行的最小路径和
	return Math.min(...matrix[m - 1]);
};

相关题目

题号	标题	题解	标签	难度	力扣
1289	下降路径最小和 II		数组 动态规划 矩阵	🔴	🀄️ 🔗