951. 翻转等价二叉树

🟠   🔖  树 深度优先搜索 二叉树  🔗 力扣 LeetCode

题目

For a binary tree T , we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.

A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.

Given the roots of two binary trees root1 and root2, return true if the two trees are flip equivalent or false otherwise.

Example 1:

Flipped Trees Diagram

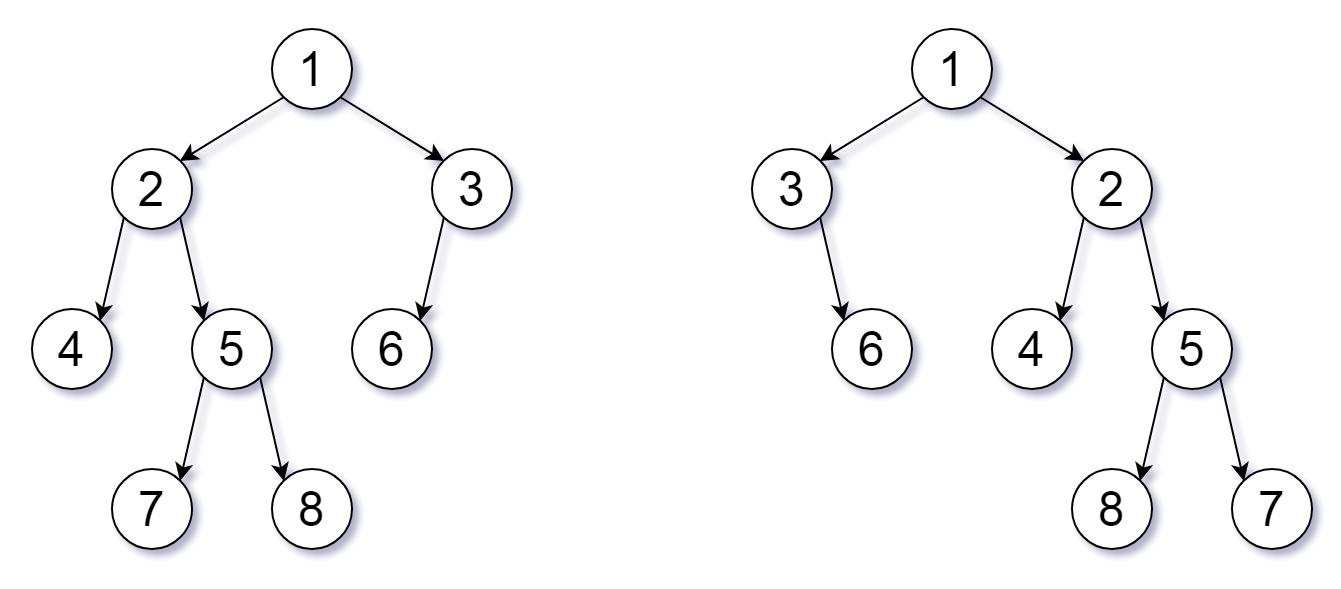
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]

Output: true

Explanation: We flipped at nodes with values 1, 3, and 5.

Example 2:

Input: root1 = [], root2 = []

Output: true

Example 3:

Input: root1 = [], root2 = [1]

Output: false

Constraints:

• The number of nodes in each tree is in the range [0, 100].
• Each tree will have unique node values in the range [0, 99].

题目大意

我们可以为二叉树 T 定义一个 翻转操作，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y ，我们就称二叉树 X 翻转等价 于二叉树 Y 。

这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是 翻转等价 的函数，则返回 true ，否则返回 false 。

示例 1：

Flipped Trees Diagram

输入： root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]

输出： true

解释： 我们翻转值为 1，3 以及 5 的三个节点。

示例 2:

输入: root1 = [], root2 = []

输出: true

示例 3:

输入: root1 = [], root2 = [1]

输出: false

提示：

• 每棵树节点数在 [0, 100] 范围内
• 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数

解题思路

翻转等价的定义意味着可以通过一系列的翻转操作，使得两个二叉树结构相同，可以使用递归的方法来解决这个问题。

1. 递归比较：递归比较两个节点的值和结构:

   • 如果两个节点都为 null，返回 true，表示两个树在这一位置相同；
   • 如果只有一个节点为 null，返回 false，表示树结构不同；
   • 如果两个节点的值不相等，直接返回 false；
   • 如果两个节点的值相等，则递归检查左右子树；

2. 递归检查子树：

   • 对于当前节点的左右子树，可以有两种比较方式：
     • 不翻转：直接比较左子树与左子树，右子树与右子树。
     • 翻转：比较左子树与右子树，右子树与左子树。
   • 如果两种方式中任意一种成立，则返回 true。

复杂度分析

• 时间复杂度：O(n)，在最坏情况下，需要访问每个节点一次。
• 空间复杂度：O(h)，其中 h 是树的高度。使用了递归，递归调用栈的深度与树的高度有关：
  • 在平衡的情况下，空间复杂度是 O(log n)；
  • 而在极度不平衡的情况下（如链表），空间复杂度为 O(n)。

代码

/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {boolean}
 */
var flipEquiv = function (root1, root2) {
	if (!root1 && !root2) return true; // 都是 null
	if (!root1 || !root2) return false; // 其中一个是 null
	if (root1.val !== root2.val) return false; // 检查当前节点的值是否相等

	// 检查左右子树是否相等（翻转 or 不翻转）
	return (
		(flipEquiv(root1.left, root2.left) &&
			flipEquiv(root1.right, root2.right)) ||
		(flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left))
	);
};