684. 冗余连接

🟠   🔖  深度优先搜索 广度优先搜索 并查集 图  🔗 力扣 LeetCode

题目

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree ofn nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

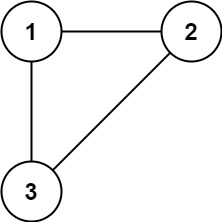
Input: edges = [[1,2],[1,3],[2,3]]

Output: [2,3]

Example 2:

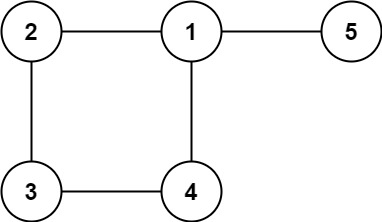
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]

Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

题目大意

树可以看成是一个连通且 无环的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

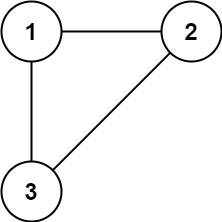
输入: edges = [[1,2], [1,3], [2,3]]

输出: [2,3]

示例 2：

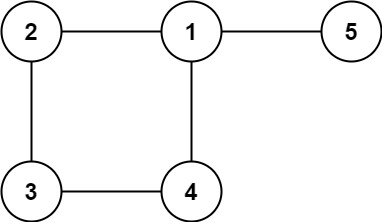
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]

输出: [1,4]

提示:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges 中无重复元素
• 给定的图是连通的

解题思路

1. 定义数据结构

   • 使用 邻接表 (graph) 来表示无向图，使用 Map 存储每个节点及其相邻节点列表。。
   • 定义辅助函数 dfs(u, target, visited)，用于判断从节点 u 出发是否能到达 target。

2. 环检测逻辑

   • 遍历 edges 数组，对于每一条边 [u, v]：
     • 如果 u 和 v 已经连通（即在当前图中存在路径），说明这条边是冗余边，直接返回 [u, v]。
     • 否则，将这条边加入图中（即更新邻接表）。

3. DFS 实现

   • 递归判断当前节点是否可以通过未访问过的节点到达目标节点：
     • 如果到达目标节点，说明这条边形成了环，返回 true。
     • 否则递归继续搜索邻居节点。

复杂度分析

• 时间复杂度：O(n^2)，在最坏情况下，需要遍历每条边并进行 DFS 搜索，每次搜索可能遍历所有节点。
• 空间复杂度：O(n)，邻接表和递归栈的空间开销。

代码

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function (edges) {
	const graph = new Map(); // 图的邻接表

	// DFS 判断节点 u 是否能够到达目标节点 target
	const dfs = (u, target, visited) => {
		if (u === target) return true; // 找到目标节点
		visited.add(u); // 标记节点已访问
		for (let neighbor of graph.get(u) || []) {
			if (!visited.has(neighbor) && dfs(neighbor, target, visited)) return true;
		}
		return false; // 未找到目标节点
	};

	for (let [u, v] of edges) {
		// 判断是否形成环
		if (graph.has(u) && graph.has(v)) {
			const visited = new Set();
			if (dfs(u, v, visited)) return [u, v]; // 找到冗余边
		}

		// 将边加入图中
		if (!graph.has(u)) graph.set(u, []);
		if (!graph.has(v)) graph.set(v, []);
		graph.get(u).push(v);
		graph.get(v).push(u);
	}
};

相关题目

题号	标题	题解	标签	难度	力扣
685	冗余连接 II		深度优先搜索 广度优先搜索 并查集 1+	🔴	🀄️ 🔗
721	账户合并		深度优先搜索 广度优先搜索 并查集 4+	🟠	🀄️ 🔗
2127	参加会议的最多员工数		深度优先搜索 图 拓扑排序	🔴	🀄️ 🔗
2608	图中的最短环		广度优先搜索 图	🔴	🀄️ 🔗