662. 二叉树最大宽度
662. 二叉树最大宽度
🟠 🔖 树 深度优先搜索 广度优先搜索 二叉树 🔗 力扣 LeetCode
题目
Given the root of a binary tree, return themaximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end- nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
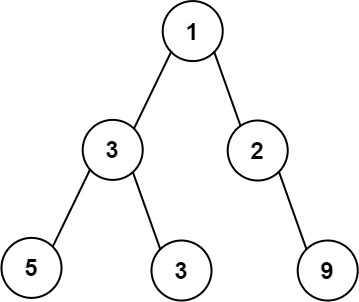
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:

Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
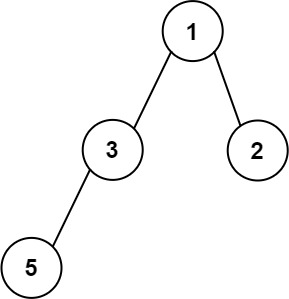
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
题目大意
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1:

输入: root = [1,3,2,5,3,null,9]
输出: 4
解释: 最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
示例 2:

输入: root = [1,3,2,5,null,null,9,6,null,7]
输出: 7
解释: 最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。
示例 3:

输入: root = [1,3,2,5]
输出: 2
解释: 最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。
提示:
- 树中节点的数目范围是
[1, 3000] -100 <= Node.val <= 100
解题思路
这道题可以通过宽度优先搜索(BFS)来解决,借助队列,可以在遍历过程中记录每个节点的位置索引,并通过计算该层最左和最右节点的索引差异来确定最大宽度。
为了方便计算节点之间的距离,给每个节点分配一个虚拟索引。假设根节点的索引为 0,对于某个节点i,其左孩子的索引为2*i + 1,右孩子的索引为2*i + 2。这样就可以在遍历的过程中记录每一层的最左和最右索引,来计算该层的宽度:宽度 = 最右索引 - 最左索引 + 1。
- 初始化:使用队列来进行层序遍历,队列中的每个元素是一个二元组,包含节点和节点对应的索引位置。
- 遍历树的每一层:对于每一层,记录这一层的最左和最右节点的索引。
- 更新最大宽度:通过计算每层的宽度来更新最大宽度。
- 返回最大宽度:遍历完成后,返回记录的最大宽度。
复杂度分析
- 时间复杂度:
O(n),其中n是二叉树中的节点数量。我们需要遍历每一个节点一次。 - 空间复杂度:
O(n),在最坏情况下,队列中会包含最多一整层的节点数量。
代码
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var widthOfBinaryTree = function (root) {
if (!root) return 0;
let queue = [[root, 0]],
res = 0,
first,
last;
// BFS
while (queue.length) {
const len = queue.length;
// 这一层的最左节点的索引
const startIndex = queue[0][1];
for (let i = 0; i < len; i++) {
const [node, index] = queue.shift();
// 减去这一层的最左节点的索引,防止溢出
const curIndex = index - startIndex;
// 记录这一层的最左和最右节点的索引
if (i == 0) first = curIndex;
if (i == len - 1) last = curIndex;
if (node.left) queue.push([node.left, curIndex * 2 + 1]);
if (node.right) queue.push([node.right, curIndex * 2 + 2]);
}
res = Math.max(res, last - first + 1);
}
return res;
};
