2373. 矩阵中的局部最大值

🟢   🔖  数组 矩阵  🔗 力扣 LeetCode

题目

You are given an n x n integer matrix grid.

Generate an integer matrix maxLocal of size (n - 2) x (n - 2) such that:

• maxLocal[i][j] is equal to the largest value of the 3 x 3 matrix in grid centered around row i + 1 and column j + 1.

In other words, we want to find the largest value in every contiguous 3 x 3 matrix in grid.

Return the generated matrix.

Example 1:

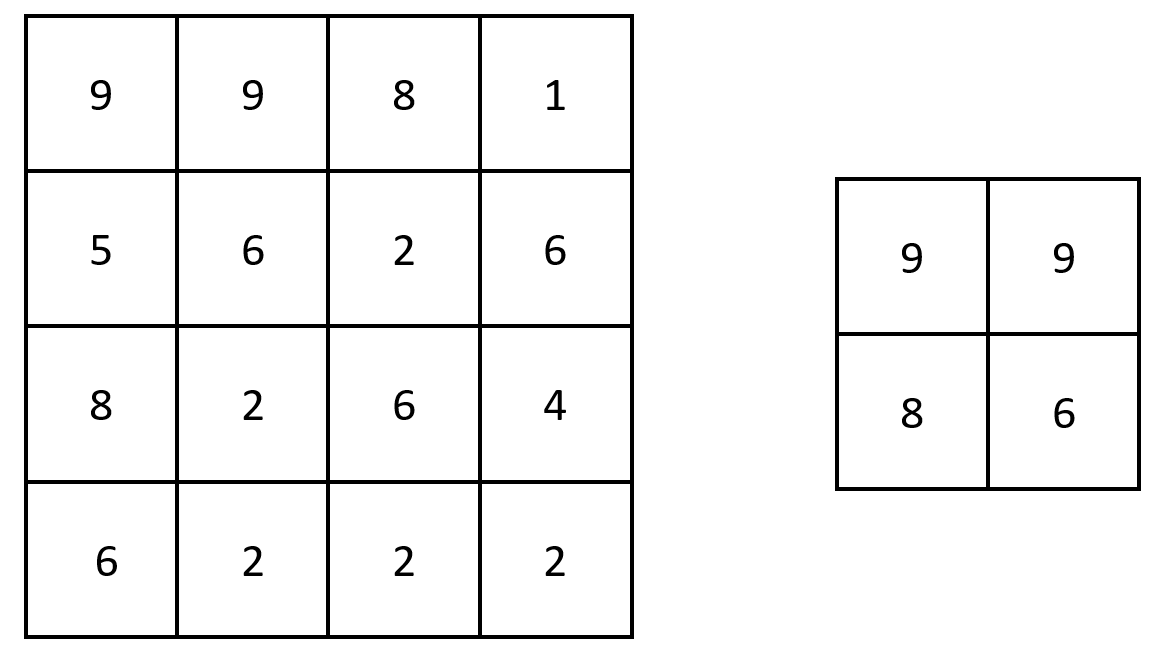
Input: grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]

Output: [[9,9],[8,6]]

Explanation: The diagram above shows the original matrix and the generated matrix.

Notice that each value in the generated matrix corresponds to the largest value of a contiguous 3 x 3 matrix in grid.

Example 2:

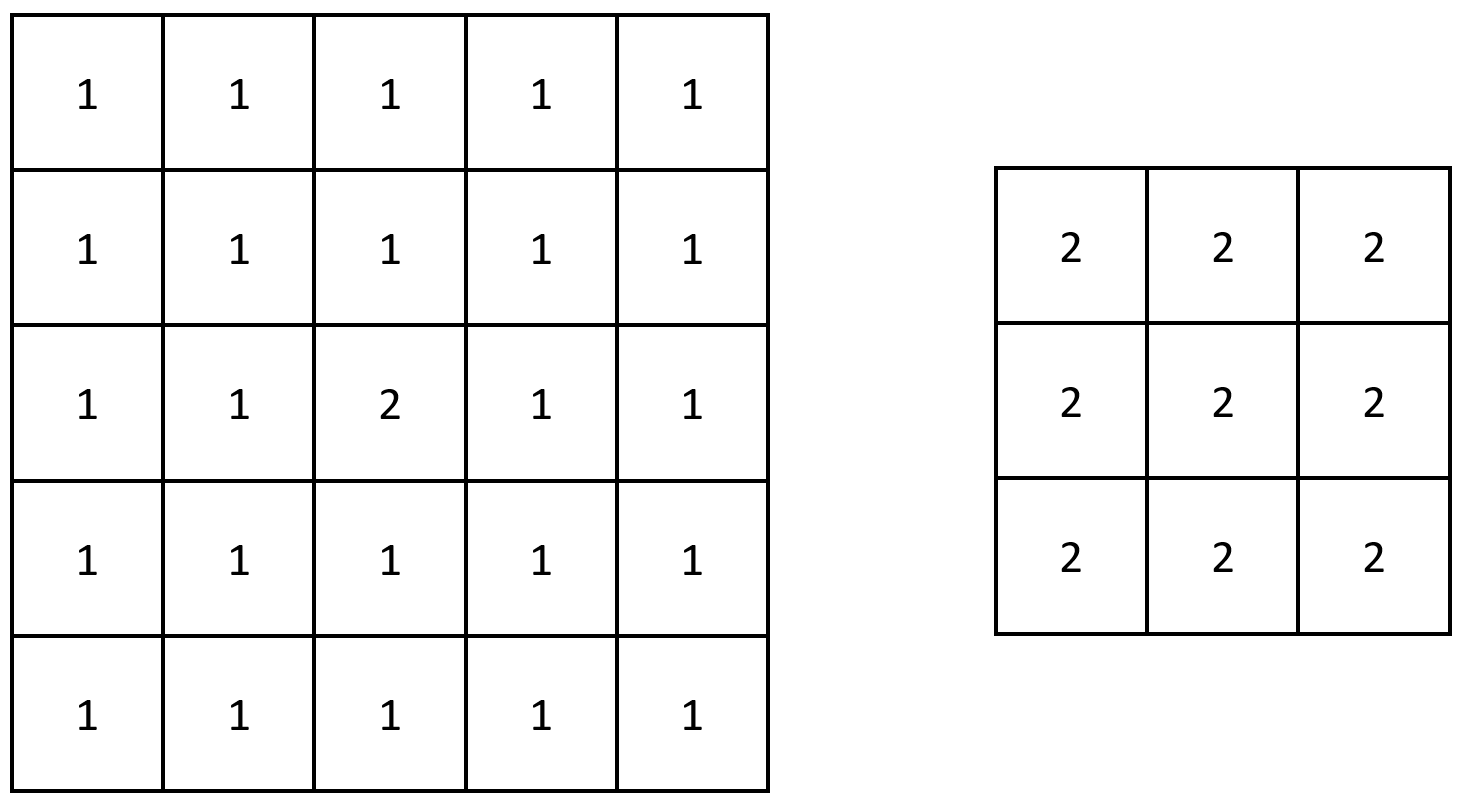
Input: grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]

Output: [[2,2,2],[2,2,2],[2,2,2]]

Explanation: Notice that the 2 is contained within every contiguous 3 x 3 matrix in grid.

Constraints:

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 1 <= grid[i][j] <= 100

题目大意

给你一个大小为 n x n 的整数矩阵 grid 。

生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ，并满足：

• maxLocal[i][j] 等于 grid 中以 i + 1 行和 j + 1 列为中心的 3 x 3 矩阵中的 最大值 。

换句话说，我们希望找出 grid 中每个 3 x 3 矩阵中的最大值。

返回生成的矩阵。

示例 1：

输入： grid = [[9,9,8,1],[5,6,2,6],[8,2,6,4],[6,2,2,2]]

输出：[[9,9],[8,6]]

解释： 原矩阵和生成的矩阵如上图所示。

注意，生成的矩阵中，每个值都对应 grid 中一个相接的 3 x 3 矩阵的最大值。

示例 2：

输入： grid = [[1,1,1,1,1],[1,1,1,1,1],[1,1,2,1,1],[1,1,1,1,1],[1,1,1,1,1]]

输出：[[2,2,2],[2,2,2],[2,2,2]]

解释： 注意，2 包含在 grid 中每个 3 x 3 的矩阵中。

提示：

• n == grid.length == grid[i].length
• 3 <= n <= 100
• 1 <= grid[i][j] <= 100

解题思路

1. 辅助函数：

   • 使用一个辅助函数 findMax(x, y)，从位置 (x, y) 开始遍历从 (x, y) 到 (x+2, y+2) 的 3x3 子网格，计算最大值。

2. 遍历网格：

   • 子网格从左上角开始，右下角结束，总共有 (n-2) x (n-2) 个 3x3 子网格。
   • 遍历原始网格中的所有可能的 3x3 子网格，逐个计算子网格中的最大值。
   • 创建一个新的网格 res，存储每个子网格的最大值。

复杂度分析

• 时间复杂度：O(n^2)
  • findMax 每次需要遍历 3x3 网格，复杂度为 O(1)。
  • 总共有 (n-2) x (n-2) 个子网格，每个子网格调用一次 findMax。
  • 总体复杂度为 O((n-2)^2)。
• 空间复杂度：O((n-2)^2)，创建了一个大小为 (n-2) x (n-2) 的二维数组。

代码

/**
 * @param {number[][]} grid
 * @return {number[][]}
 */
var largestLocal = function (grid) {
	const findMax = (x, y) => {
		let max = 0; // 初始化最大值
		for (let i = x; i < x + 3; i++) {
			for (let j = y; j < y + 3; j++) {
				max = Math.max(max, grid[i][j]); // 更新最大值
			}
		}
		return max;
	};

	const n = grid.length; // 原网格的大小
	let res = new Array(n - 2).fill().map(() => new Array(n - 2)); // 结果网格

	// 遍历所有可能的起始点
	for (let i = 0; i < n - 2; i++) {
		for (let j = 0; j < n - 2; j++) {
			res[i][j] = findMax(i, j); // 计算对应位置的最大值
		}
	}

	return res;
};