2684. 矩阵中移动的最大次数

🟠   🔖  数组 动态规划 矩阵  🔗 力扣 LeetCode

题目

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

Example 1:

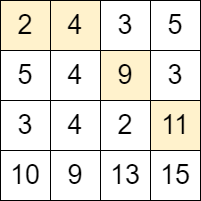
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]

Output: 3

Explanation: We can start at the cell (0, 0) and make the following moves:

• (0, 0) -> (0, 1).
• (0, 1) -> (1, 2).
• (1, 2) -> (2, 3).

It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]

Output: 0

Explanation: Starting from any cell in the first column we cannot perform any moves.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10^5
• 1 <= grid[i][j] <= 10^6

题目大意

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

• 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

输入： grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]

输出： 3

解释： 可以从单元格 (0, 0) 开始并且按下面的路径移动：

• (0, 0) -> (0, 1).
• (0, 1) -> (1, 2).
• (1, 2) -> (2, 3).

可以证明这是能够移动的最大次数。

示例 2：

输入： grid = [[3,2,4],[2,1,9],[1,1,7]]

输出： 0

解释： 从第一列的任一单元格开始都无法移动。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10^5
• 1 <= grid[i][j] <= 10^6

解题思路

可以使用动态规划来计算从矩阵第一列的任一单元格出发，能够移动的最大次数。

思路一：动态规划

1. 初始化状态： 创建一个 dp 数组，其中 dp[i][j] 表示从单元格 (i, j) 开始能够移动的最大次数。初始时，所有单元格的最大移动次数都设为 0，因为矩阵的最后一列没有后续的单元格可移动，移动次数就是 0。

2. 倒序遍历列：

   从矩阵的倒数第二列开始遍历，直到第一列。在每一列中，我们都要计算从这一列每个单元格可以向右移动到下一列的次数。

3. 检查可移动条件：

   • 对于每个单元格 (i, j)，检查以下三个方向是否满足移动条件：
     • 移动到上右 (i - 1, j + 1)，如果 i > 0 并且 grid[i][j] < grid[i - 1][j + 1]，则可以移动，更新移动次数。
     • 移动到右 (i, j + 1)，如果 grid[i][j] < grid[i][j + 1]，则可以移动，更新移动次数。
     • 移动到下右 (i + 1, j + 1)，如果 i < m - 1 并且 grid[i][j] < grid[i + 1][j + 1]，则可以移动，更新移动次数。

4. 获取结果：

   • 最后， dp[i][0] 中存储的就是从第一列任一单元格出发，能够移动的最大次数，从中获取最大的移动次数，作为结果返回。

复杂度分析

• 时间复杂度：O(m * n)，其中 m、n 分别是矩阵的行数和列数，需要遍历整个矩阵。
• 空间复杂度：O(m * n)，用于存储 dp 数组。

思路二：压缩状态的动态规划

1. 初始化状态： 使用一个一维数组 dp，长度为 m，表示从每一行的某一列出发，能够到达的最大移动次数。最开始，dp[i] 表示从最后一列的第 i 行出发时的移动次数，因为没有后续的单元格可移动，初始值为 0。

2. 倒序遍历列：

   从矩阵的倒数第二列开始遍历，直到第一列。在每一列中，我们都要计算从这一列每个单元格可以向右移动到下一列的次数。

3. 检查可移动条件：

   • 对于每个单元格 (i, j)，检查以下三个方向是否满足移动条件：
     • 移动到上右 (i - 1, j + 1)，如果 i > 0 并且 grid[i][j] < grid[i - 1][j + 1]，则可以移动，更新移动次数。
     • 移动到右 (i, j + 1)，如果 grid[i][j] < grid[i][j + 1]，则可以移动，更新移动次数。
     • 移动到下右 (i + 1, j + 1)，如果 i < m - 1 并且 grid[i][j] < grid[i + 1][j + 1]，则可以移动，更新移动次数。

4. 更新状态数组：

   • 因为后续计算还依赖下一列的移动次数，所以需要通过临时数组 newDp 存储当前列的移动次数，在遍历完当前列后，更新 dp 为 newDp。

5. 获取结果：

   • 最后， dp 数组中存储的就是从第一列任一单元格出发，能够移动的最大次数，从 dp 数组中获取最大的移动次数，作为结果返回。

复杂度分析

• 时间复杂度：O(m * n)，其中 m、n 分别是矩阵的行数和列数，需要遍历整个矩阵。
• 空间复杂度：O(m)，只需要一个一维数组 dp 存储状态。

代码

动态规划

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxMoves = function (grid) {
	const m = grid.length,
		n = grid[0].length;
	// 创建 dp 数组
	const dp = new Array(m).fill(0).map((i) => new Array(n).fill(0));

	// 倒序遍历列
	for (let j = n - 2; j >= 0; j--) {
		for (let i = 0; i < m; i++) {
			// 检查上右、右、下右三个方向
			if (i > 0 && grid[i][j] < grid[i - 1][j + 1]) {
				dp[i][j] = Math.max(dp[i][j], dp[i - 1][j + 1] + 1);
			}
			if (grid[i][j] < grid[i][j + 1]) {
				dp[i][j] = Math.max(dp[i][j], dp[i][j + 1] + 1);
			}
			if (i < m - 1 && grid[i][j] < grid[i + 1][j + 1]) {
				dp[i][j] = Math.max(dp[i][j], dp[i + 1][j + 1] + 1);
			}
		}
	}
	// 获取结果
	let maxMoves = 0;
	for (let i = 0; i < m; i++) {
		maxMoves = Math.max(maxMoves, dp[i][0]);
	}
	return maxMoves;
};

压缩状态的动态规划

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxMoves = function (grid) {
	const m = grid.length,
		n = grid[0].length;
	// 初始化 dp 数组
	let dp = new Array(m).fill(0);

	for (let j = n - 2; j >= 0; j--) {
		// 记录当前列的 dp 数组
		let newDp = [];
		for (let i = 0; i < m; i++) {
			// 当前单元格的移动次数
			let moves = 0;
			// 检查三个可移动方向
			if (i > 0 && grid[i][j] < grid[i - 1][j + 1]) {
				moves = Math.max(moves, dp[i - 1] + 1);
			}
			if (grid[i][j] < grid[i][j + 1]) {
				moves = Math.max(moves, dp[i] + 1);
			}
			if (i < m - 1 && grid[i][j] < grid[i + 1][j + 1]) {
				moves = Math.max(moves, dp[i + 1] + 1);
			}
			// 更新当前列的移动次数
			newDp.push(moves);
		}
		// 更新 dp 数组
		dp = newDp;
	}
	// 返回最大的移动次数
	return Math.max(...dp);
};