2103. 环和杆

🟢   🔖  哈希表 字符串  🔗 力扣 LeetCode

题目

There are n rings and each ring is either red, green, or blue. The rings are distributed across ten rods labeled from 0 to 9.

You are given a string rings of length 2n that describes the n rings that are placed onto the rods. Every two characters in rings forms a color-position pair that is used to describe each ring where:

• The first character of the ith pair denotes the ith ring's color ('R', 'G', 'B').
• The second character of the ith pair denotes the rod that the ith ring is placed on ('0' to '9').

For example, "R3G2B1" describes n == 3 rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.

Return the number of rods that have all three colors of rings on them.

Example 1:

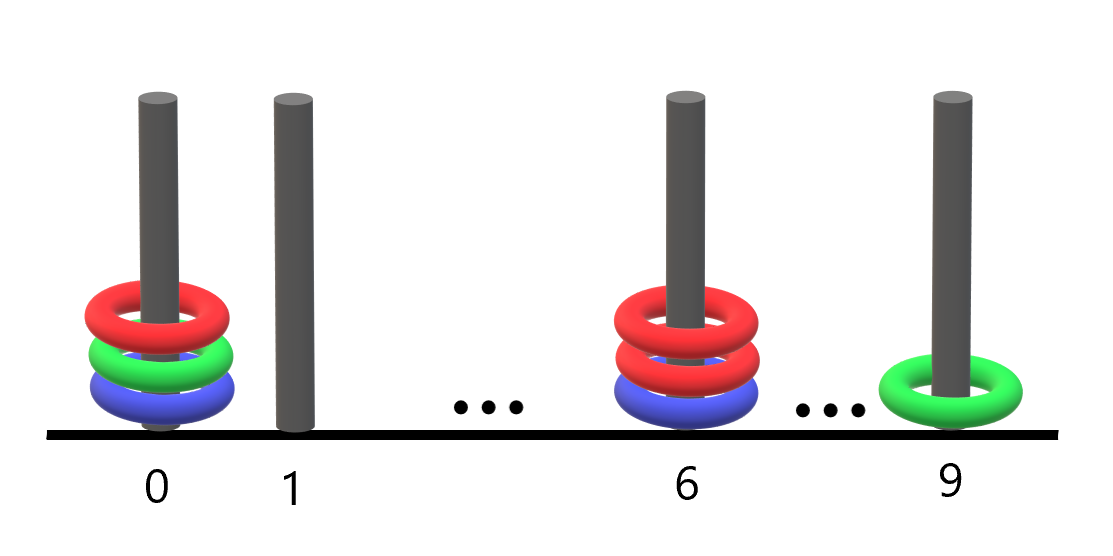
Input: rings = "B0B6G0R6R0R6G9"

Output: 1

Explanation:

• The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
• The rod labeled 6 holds 3 rings, but it only has red and blue.
• The rod labeled 9 holds only a green ring.

Thus, the number of rods with all three colors is 1.

Example 2:

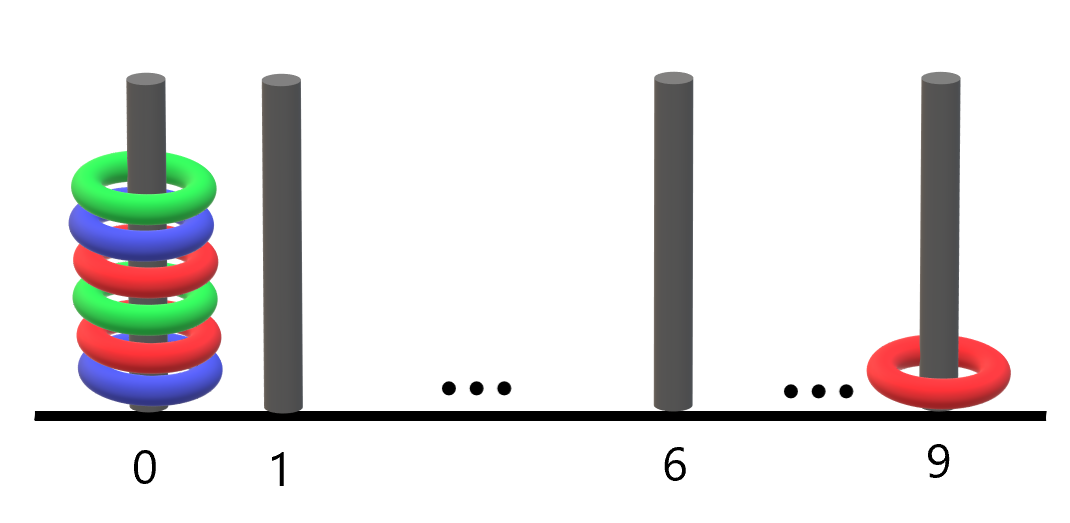
Input: rings = "B0R0G0R9R0B0G0"

Output: 1

Explanation:

• The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
• The rod labeled 9 holds only a red ring.

Thus, the number of rods with all three colors is 1.

Example 3:

Input: rings = "G4"

Output: 0

Explanation:

Only one ring is given. Thus, no rods have all three colors.

Constraints:

• rings.length == 2 * n
• 1 <= n <= 100
• rings[i] where i is even is either 'R', 'G', or 'B' (0-indexed).
• rings[i] where i is odd is a digit from '0' to '9' (0-indexed).

题目大意

总计有 n 个环，环的颜色可以是红、绿、蓝中的一种。这些环分别穿在 10 根编号为 0 到 9 的杆上。

给你一个长度为 2n 的字符串 rings ，表示这 n 个环在杆上的分布。rings 中每两个字符形成一个 颜色位置对 ，用于描述每个环：

• 第 i 对中的 第一个 字符表示第 i 个环的 颜色 （'R'、'G'、'B'）。
• 第 i 对中的 第二个 字符表示第 i 个环的 位置 ，也就是位于哪根杆上（'0' 到 '9'）。

例如，"R3G2B1" 表示：共有 n == 3 个环，红色的环在编号为 3 的杆上，绿色的环在编号为 2 的杆上，蓝色的环在编号为 1 的杆上。

找出所有集齐 全部三种颜色 环的杆，并返回这种杆的数量。

示例 1：

输入： rings = "B0B6G0R6R0R6G9"

输出： 1

解释：

• 编号 0 的杆上有 3 个环，集齐全部颜色：红、绿、蓝。
• 编号 6 的杆上有 3 个环，但只有红、蓝两种颜色。
• 编号 9 的杆上只有 1 个绿色环。

因此，集齐全部三种颜色环的杆的数目为 1 。

示例 2：

输入： rings = "B0R0G0R9R0B0G0"

输出： 1

解释：

• 编号 0 的杆上有 6 个环，集齐全部颜色：红、绿、蓝。
• 编号 9 的杆上只有 1 个红色环。

因此，集齐全部三种颜色环的杆的数目为 1 。

示例 3：

输入： rings = "G4"

输出： 0

解释：

只给了一个环，因此，不存在集齐全部三种颜色环的杆。

提示：

• rings.length == 2 * n
• 1 <= n <= 100
• 如 i 是 偶数 ，则 rings[i] 的值可以取 'R'、'G' 或 'B'（下标从 0 开始计数）
• 如 i 是 奇数 ，则 rings[i] 的值可以取 '0' 到 '9' 中的一个数字（下标从 0 开始计数）

解题思路

1. 使用位运算表示颜色:

   • 每种颜色用一个二进制位表示：
     • 红色 (R): 1 (二进制 001)
     • 绿色 (G): 2 (二进制 010)
     • 蓝色 (B): 4 (二进制 100)
   • 如果一个柱子上同时拥有这三种颜色，其状态的二进制表示为 111，对应十进制值 7。

2. 初始化柱子状态:

   • 使用长度为 10 的数组 count，初始值为 0，表示每个柱子上没有任何颜色的环。

3. 遍历输入字符串:

   • rings 中，每两个字符表示一个环的颜色和柱子编号。
   • 遍历字符串，将颜色用位运算累加到对应柱子的状态中：
     • count[pillar] |= colorValue 将颜色信息叠加到柱子的状态。

4. 统计满足条件的柱子:

   • 遍历 count 数组，统计状态为 7 的柱子数量，即包含三种颜色的柱子。

复杂度分析

• 时间复杂度：O(n)
  • 遍历 rings 一次，时间复杂度为 O(n)，其中 n 是字符串的长度。
  • 遍历 count 数组进行统计，时间复杂度为 O(1)（数组长度固定为 10）。
  • 总时间复杂度为 O(n)。
• 空间复杂度：O(1)，使用了一个固定大小为 10 的数组 count。

代码

/**
 * @param {string} rings
 * @return {number}
 */
var countPoints = function (rings) {
	const colorMap = {
		R: 1,
		G: 2,
		B: 4
	};
	let count = new Array(10).fill(0);
	for (let i = 0; i < rings.length; i += 2) {
		count[Number(rings[i + 1])] |= colorMap[rings[i]];
	}
	return count.filter((i) => i == 7).length;
};

相关题目

题号	标题	题解	标签	难度	力扣
1941	检查是否所有字符出现次数相同	[✓]	哈希表 字符串 计数	🟢	🀄️ 🔗