2924. 找到冠军 II
2924. 找到冠军 II
题目
There are n teams numbered from 0 to n - 1 in a tournament; each team is also a node in a DAG.
You are given the integer n and a 0-indexed 2D integer array edges of length m representing the DAG , where edges[i] = [ui, vi] indicates that there is a directed edge from team ui to team vi in the graph.
A directed edge from a to b in the graph means that team a is stronger than team b and team b is weaker than team a.
Team a will be the champion of the tournament if there is no team b that is stronger than team a.
Return the team that will be thechampion of the tournament if there is a unique champion, otherwise, return -1.
Notes
- A cycle is a series of nodes
a1, a2, ..., an, an+1such that nodea1is the same node as nodean+1, the nodesa1, a2, ..., anare distinct, and there is a directed edge from the nodeaito nodeai+1for everyiin the range[1, n]. - A DAG is a directed graph that does not have any cycle.
Example 1:
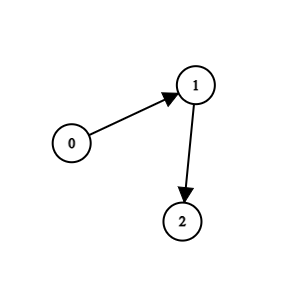
Input: n = 3, edges = [[0,1],[1,2]]
Output: 0
Explanation: Team 1 is weaker than team 0. Team 2 is weaker than team 1. So the champion is team 0.
Example 2:
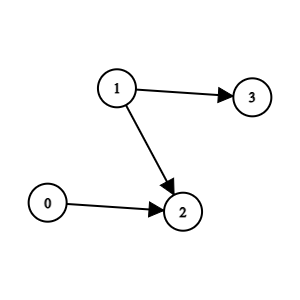
Input: n = 4, edges = [[0,2],[1,3],[1,2]]
Output: -1
Explanation: Team 2 is weaker than team 0 and team 1. Team 3 is weaker than team 1. But team 1 and team 0 are not weaker than any other teams. So the answer is -1.
Constraints:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]- The input is generated such that if team
ais stronger than teamb, teambis not stronger than teama. - The input is generated such that if team
ais stronger than teamband teambis stronger than teamc, then teamais stronger than teamc.
题目大意
一场比赛中共有 n 支队伍,按从 0 到 n - 1 编号。每支队伍也是 有向无环图(DAG) 上的一个节点。
给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图,其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。
从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ,也就是 b 队比 a 队 弱 。
在这场比赛中,如果不存在某支强于 a 队的队伍,则认为 a 队将会是 冠军 。
如果这场比赛存在 唯一 一个冠军,则返回将会成为冠军的队伍。否则,返回 -1。
注意
- 环 是形如
a1, a2, ..., an, an+1的一个序列,且满足:节点a1与节点an+1是同一个节点;节点a1, a2, ..., an互不相同;对于范围[1, n]中的每个i,均存在一条从节点ai到节点ai+1的有向边。 - 有向无环图 是不存在任何环的有向图。
示例 1:

输入: n = 3, edges = [[0,1],[1,2]]
输出: 0
解释: 1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。
示例 2:

输入: n = 4, edges = [[0,2],[1,3],[1,2]]
输出: -1
解释: 2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。
提示:
1 <= n <= 100m == edges.length0 <= m <= n * (n - 1) / 2edges[i].length == 20 <= edge[i][j] <= n - 1edges[i][0] != edges[i][1]- 生成的输入满足:如果
a队比b队强,就不存在b队比a队强 - 生成的输入满足:如果
a队比b队强,b队比c队强,那么a队比c队强
解题思路
- 使用一个集合
visited存储所有被击败的节点。 - 遍历所有边,把每条边上被击败的节点加入
visited集合中,如边(a, b),将b加入visited,表示b被a击败。 - 遍历完
edges后,如果visited集合的大小等于n - 1,则说明有一个节点没有被击败,这个节点是可能的冠军。 - 遍历
0到n-1的每个节点,如果这个节点不在visited中,说明它是唯一没有被击败的节点,因此返回它作为冠军。 - 此外,如果
visited集合的大小不等于n - 1,说明有循环存在或者冠军不唯一,此时返回-1。
复杂度分析
- 时间复杂度:
O(m + n),其中m是edges数组的长度(即比赛数量),n是节点数量。遍历edges和遍历节点的时间复杂度分别是O(m)和O(n),因此总复杂度为O(m + n)。 - 空间复杂度:
O(n),使用了一个Set来存储被击败的节点,最多需要存储n个节点。
代码
/**
* @param {number} n
* @param {number[][]} edges
* @return {number}
*/
var findChampion = function (n, edges) {
let visited = new Set();
// 记录所有被击败的节点
for (let edge of edges) {
visited.add(edge[1]);
}
// 如果被击败的节点数不是 n-1,则说明冠军不存在
if (visited.size !== n - 1) {
return -1;
}
// 查找没有被击败的节点,返回该节点
for (let i = 0; i < n; i++) {
if (!visited.has(i)) {
return i;
}
}
};
