2257. 统计网格图中没有被保卫的格子数

🟠   🔖  数组 矩阵 模拟  🔗 力扣 LeetCode

题目

You are given two integers m and n representing a 0-indexed m x n grid. You are also given two 2D integer arrays guards and walls where guards[i] = [rowi, coli] and walls[j] = [rowj, colj] represent the positions of the ith guard and jth wall respectively.

A guard can see every cell in the four cardinal directions (north, east, south, or west) starting from their position unless obstructed by a wall or another guard. A cell is guarded if there is at least one guard that can see it.

Return the number of unoccupied cells that are not guarded.

Example 1:

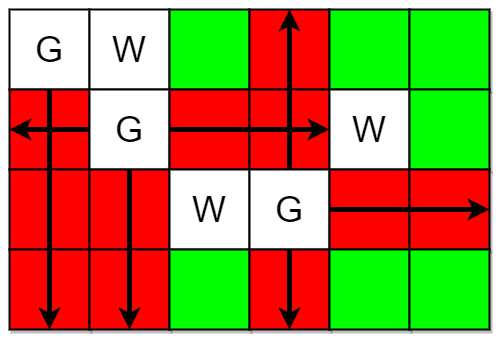
Input: m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]

Output: 7

Explanation: The guarded and unguarded cells are shown in red and green respectively in the above diagram.

There are a total of 7 unguarded cells, so we return 7.

Example 2:

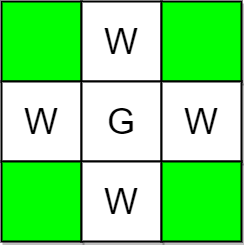
Input: m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]

Output: 4

Explanation: The unguarded cells are shown in green in the above diagram.

There are a total of 4 unguarded cells, so we return 4.

Constraints:

• 1 <= m, n <= 10^5
• 2 <= m * n <= 10^5
• 1 <= guards.length, walls.length <= 5 * 10^4
• 2 <= guards.length + walls.length <= m * n
• guards[i].length == walls[j].length == 2
• 0 <= rowi, rowj < m
• 0 <= coli, colj < n
• All the positions in guards and walls are unique.

题目大意

给你两个整数 m 和 n 表示一个下标从 0 开始的 m x n 网格图。同时给你两个二维整数数组 guards 和 walls ，其中 guards[i] = [rowi, coli] 且 walls[j] = [rowj, colj] ，分别表示第 i 个警卫和第 j 座墙所在的位置。

一个警卫能看到 4 个坐标轴方向（即东、南、西、北）的 所有 格子，除非他们被一座墙或者另外一个警卫 挡住 了视线。如果一个格子能被 至少 一个警卫看到，那么我们说这个格子被 保卫 了。

请你返回空格子中，有多少个格子是 没被保卫 的。

示例 1：

输入： m = 4, n = 6, guards = [[0,0],[1,1],[2,3]], walls = [[0,1],[2,2],[1,4]]

输出： 7

解释： 上图中，被保卫和没有被保卫的格子分别用红色和绿色表示。

总共有 7 个没有被保卫的格子，所以我们返回 7 。

示例 2：

输入： m = 3, n = 3, guards = [[1,1]], walls = [[0,1],[1,0],[2,1],[1,2]]

输出： 4

解释： 上图中，没有被保卫的格子用绿色表示。

总共有 4 个没有被保卫的格子，所以我们返回 4 。

提示：

• 1 <= m, n <= 10^5
• 2 <= m * n <= 10^5
• 1 <= guards.length, walls.length <= 5 * 10^4
• 2 <= guards.length + walls.length <= m * n
• guards[i].length == walls[j].length == 2
• 0 <= rowi, rowj < m
• 0 <= coli, colj < n
• guards 和 walls 中所有位置 互不相同 。

解题思路

1. 数据初始化

• 使用一个二维数组 g 表示网格状态：
  • 0：当前格子未被保卫；
  • 1：当前格子被守卫保卫；
  • 2：当前格子是守卫或墙。
• 将 guards 和 walls 的位置初始化为 2。

2. 模拟守卫的视线

• 遍历每个守卫 (gx, gy)，从其位置向四个方向（上下左右）扩展，直到：
  • 超出边界；
  • 遇到墙或其他守卫（值为 2）。
• 对每个可以扩展的格子，标记为 1（被保卫）。

3. 统计未被保卫的格子

• 遍历整个网格，统计值为 0 的格子数，即未被保卫的格子。

复杂度分析

• 时间复杂度：O(k * max(m, n) + m * n)。
  • 遍历 guards 和其四个方向扩展的操作，复杂度约为 O(k * max(m, n))，其中 k 是守卫的数量；
  • 统计未被保卫的格子需要遍历一次矩阵，复杂度为 O(m * n)；
  • 总复杂度为 O(k * max(m, n) + m * n)
• 空间复杂度：O(m * n)，需要一个二维数组 g。

代码

/**
 * @param {number} m
 * @param {number} n
 * @param {number[][]} guards
 * @param {number[][]} walls
 * @return {number}
 */
var countUnguarded = function (m, n, guards, walls) {
	// 初始化网格
	const g = new Array(m).fill().map(() => new Array(n).fill(0));

	// 设置守卫和墙的位置为 2
	for (let [x, y] of guards) {
		g[x][y] = 2;
	}
	for (let [x, y] of walls) {
		g[x][y] = 2;
	}

	// 定义四个方向
	const dirs = [
		[-1, 0],
		[1, 0],
		[0, -1],
		[0, 1]
	];

	// 遍历每个守卫，模拟其视线
	for (let [gx, gy] of guards) {
		for (let [dx, dy] of dirs) {
			let x = gx,
				y = gy;
			while (true) {
				x += dx;
				y += dy;
				// 超出边界或遇到障碍物
				if (x < 0 || y < 0 || x >= m || y >= n || g[x][y] == 2) {
					break;
				}
				// 标记当前格子为被保卫
				g[x][y] = 1;
			}
		}
	}

	// 统计未被保卫的格子数
	return g.reduce((sum, row) => sum + row.filter((i) => i == 0).length, 0);
};

相关题目

题号	标题	题解	标签	难度	力扣
361	轰炸敌人 🔒		数组 动态规划 矩阵	🟠	🀄️ 🔗
999	可以被一步捕获的棋子数		数组 矩阵 模拟	🟢	🀄️ 🔗