2.7 堆

堆的定义

定义

堆（Heap） 是一种特殊的树形数据结构，只要满足以下两点的树，就是堆：

堆是一个完全二叉树；
堆中每一个节点的值都必须大于等于（或小于等于）其子树中每个节点的值。

对于每个节点的值都大于等于子树中每个节点值的堆，叫作 大顶堆 。对于每个节点的值都小于等于子树中每个节点值的堆，叫作 小顶堆 。

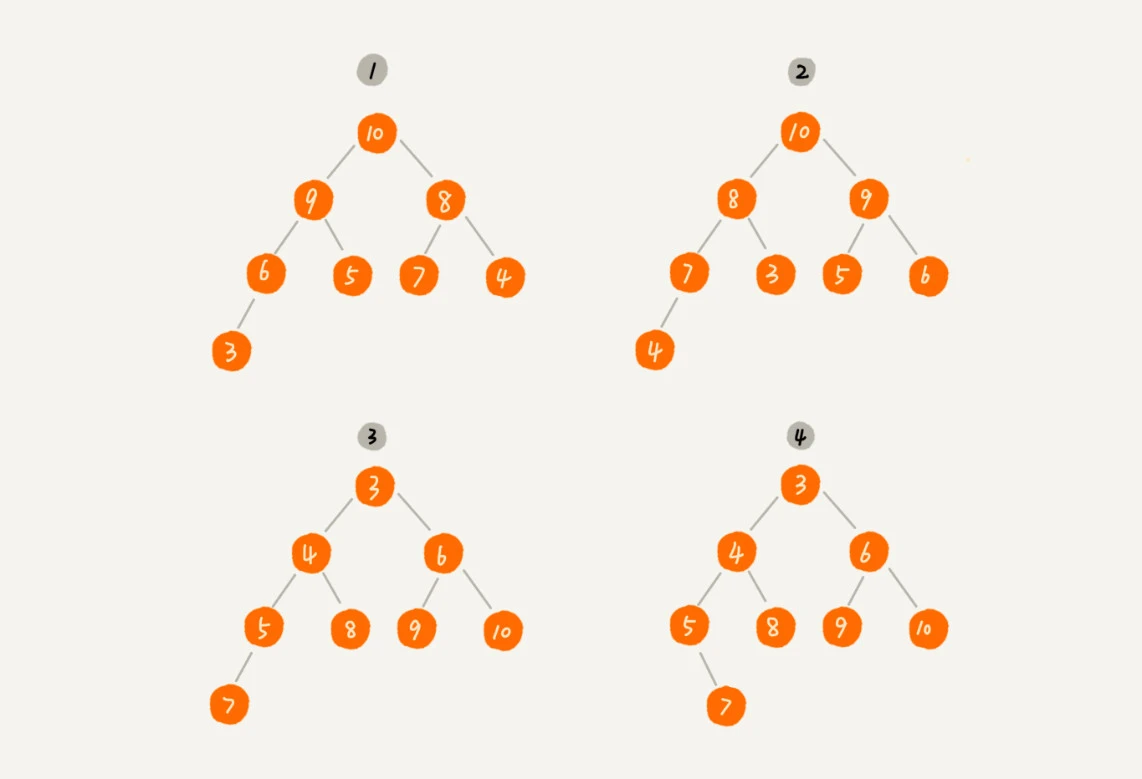
如图所示，第 1 个和第 2 个是大顶堆，第 3 个是小顶堆，第 4 个不是堆。

堆的实现

堆是一个完全二叉树，完全二叉树比较适合用数组来存储。

用数组来存储完全二叉树是非常节省存储空间的，因为不需要存储左右子节点的指针，单纯地通过数组的下标，就可以找到一个节点的左右子节点和父节点。

比如大顶堆：

可以储存为数组：[7, 5, 6, 4, 2, 1]，数组中下标为 i 的节点的左子节点，就是下标为 i * 2 + 1 的节点，右子节点就是下标为 i * 2 + 2 的节点，父节点就是下标为 Math.floor((i - 1) / 2) 的节点。

知道了如何存储一个堆，再来看看堆上有哪些操作。

1. 插入操作

插入操作是指将元素添加到堆中，并保持堆的性质。通常是将元素添加到数组的末尾，然后执行一系列比较操作，让其重新满足堆的特性，这个过程就叫做 堆化（heapify） 。

堆化实际上有两种，从下往上和从上往下。这里以从下往上的堆化方法为例。

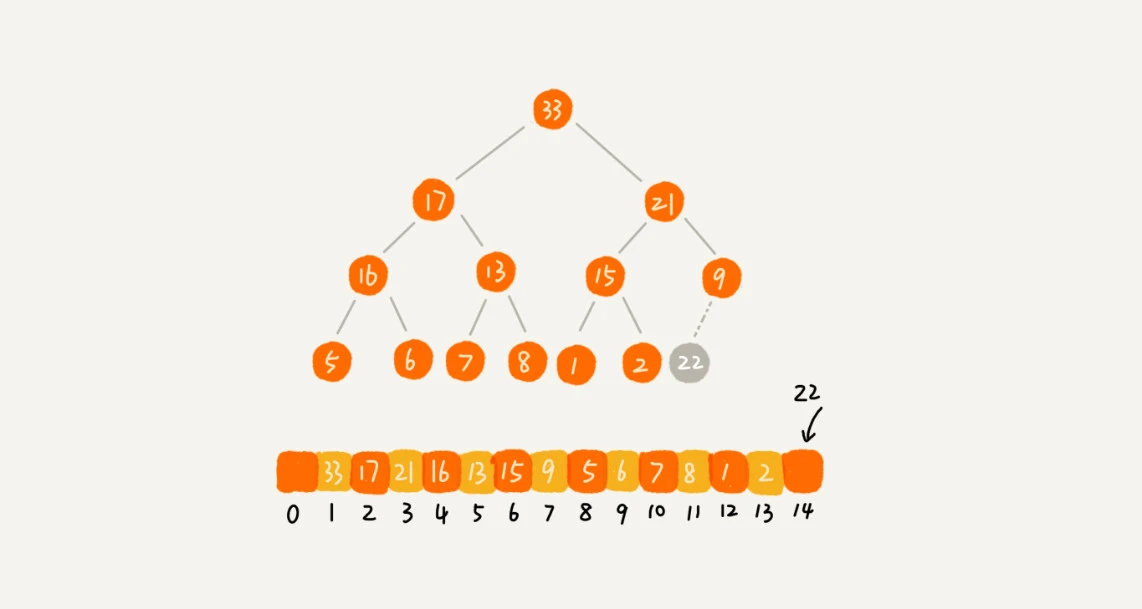
可以让新插入的节点与父节点对比大小，如果不满足子节点小于等于父节点的大小关系，就互换两个节点。一直重复这个过程，直到父子节点之间满足刚说的那种大小关系。

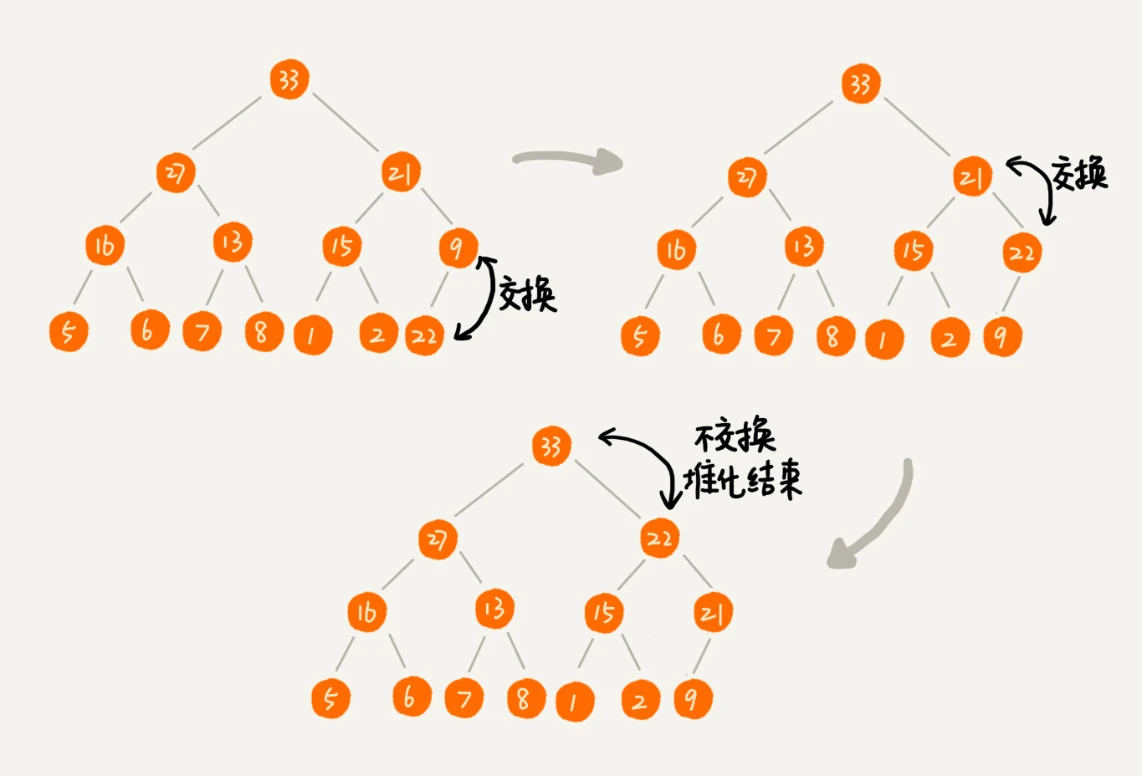
insert 函数代码如下：

class MaxHeap {
  constructor() {
    this.heap = [];
  }

  insert(value) {
    this.heap.push(value);
    this._heapifyUp();
  }

  _heapifyUp() {
    let cur = this.heap.length - 1;

    while (cur > 0) {
      const parent = Math.floor((cur - 1) / 2);
      if (this.heap[cur] > this.heap[parent]) {
        [this.heap[cur], this.heap[parent]] = [
          this.heap[parent],
          this.heap[cur],
        ];
        cur = parent;
      } else {
        break;
      }
    }
  }
}

// Example usage
const maxHeap = new MaxHeap();
maxHeap.insert(5);
maxHeap.insert(10);
maxHeap.insert(3);

console.log(maxHeap.heap); // Output: [10, 5, 3]

2. 删除操作

删除操作是指从堆中移除元素，并保持堆的性质。通常是将根节点删除，然后将最后一个节点移到根的位置，并根据堆的性质进行调整。

从堆的定义的第二条中，任何节点的值都大于等于（或小于等于）子树节点的值，可以发现，堆顶元素存储的就是堆中数据的最大值或者最小值。

假设构造的是大顶堆，堆顶元素就是最大的元素。当删除堆顶元素之后，就需要把第二大的元素放到堆顶，然后再迭代地删除第二大节点，以此类推，直到叶子节点被删除。

不过这种方法有点问题，就是最后堆化出来的堆并不满足完全二叉树的特性，会出现数组空洞。

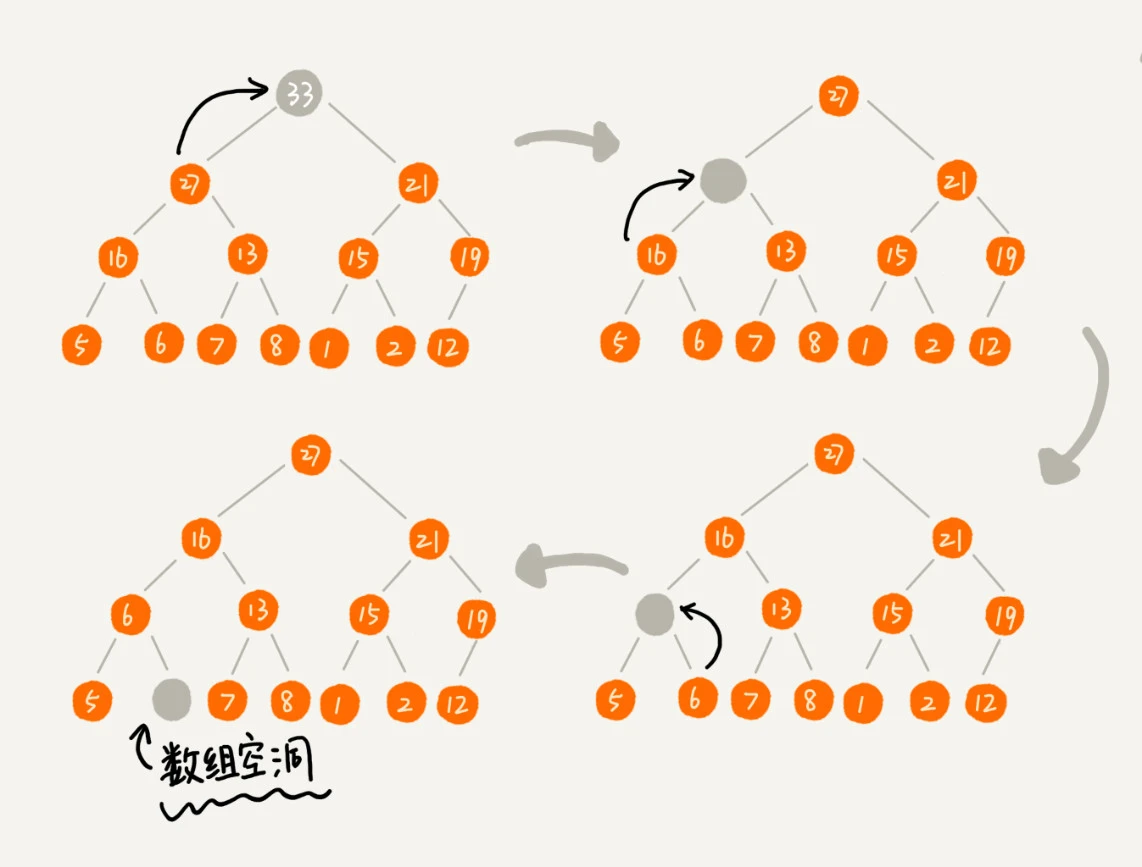
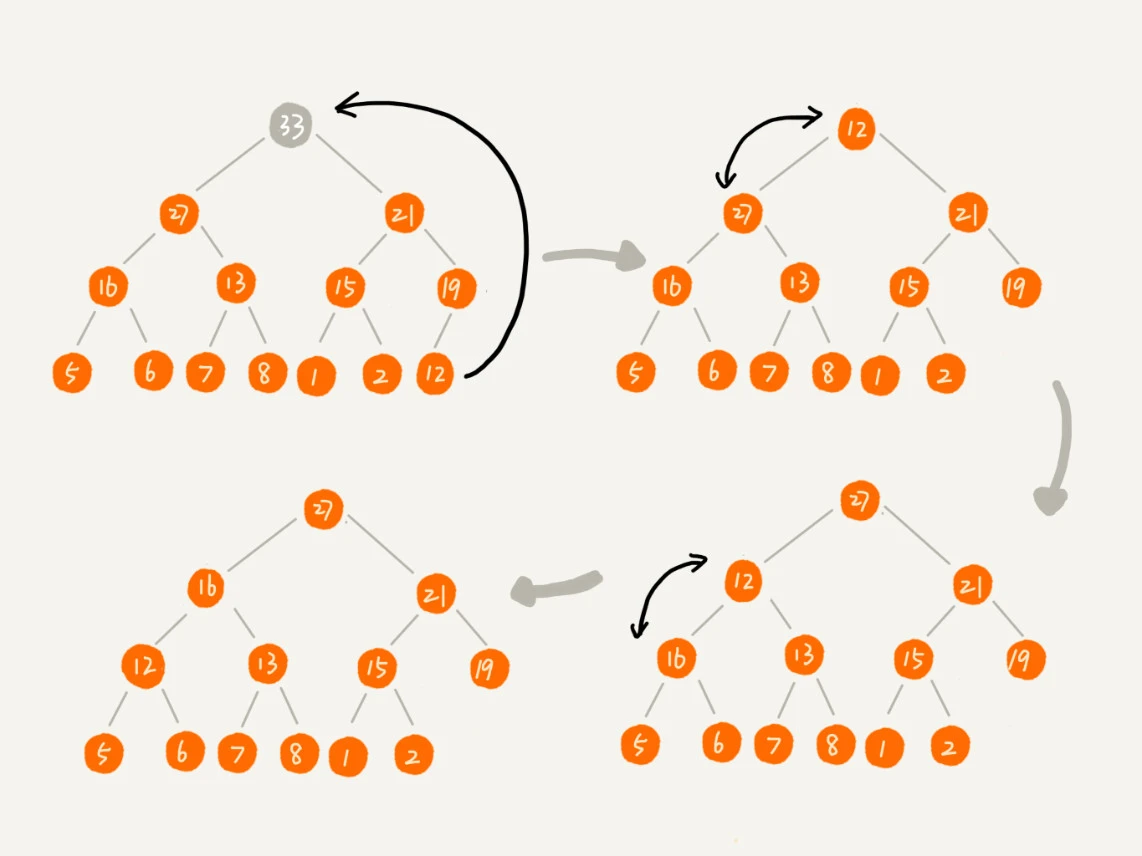
稍微改变一下思路，可以把最后一个节点放到堆顶，然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的，互换两个节点，并且重复进行这个过程，直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。

因为移除的是数组中的最后一个元素，而堆化的过程中都是交换操作，不会出现数组中的“空洞”，所以这种方法堆化之后的结果，肯定满足完全二叉树的特性。

class MaxHeap {
  // ...（之前的代码）

  extractMax() {
    if (this.heap.length === 0) {
      return null;
    }

    const max = this.heap[0];
    const last = this.heap.pop();

    if (this.heap.length > 0) {
      this.heap[0] = last;
      this._heapifyDown();
    }

    return max;
  }

  _heapifyDown() {
    let cur = 0;

    while (true) {
      const leftChild = 2 * cur + 1;
      const rightChild = 2 * cur + 2;
      let next = null;

      if (
        leftChild < this.heap.length &&
        this.heap[leftChild] > this.heap[cur]
      ) {
        next = leftChild;
      }

      if (
        rightChild < this.heap.length &&
        this.heap[rightChild] > this.heap[cur]
      ) {
        next =
          this.heap[rightChild] > this.heap[leftChild] ? rightChild : leftChild;
      }

      if (next !== null && this.heap[cur] < this.heap[next]) {
        [this.heap[cur], this.heap[next]] = [this.heap[next], this.heap[cur]];
        cur = next;
      } else {
        break;
      }
    }
  }
}

// Example usage
const maxHeap = new MaxHeap();
maxHeap.insert(5);
maxHeap.insert(10);
maxHeap.insert(3);

console.log(maxHeap.extractMax()); // Output: 10
console.log(maxHeap.heap); // Output: [5, 3]

3. 堆化操作

堆化操作是指将一个无序的数组（或者部分数组）调整为堆的过程。通常有两种堆化操作：自顶向下的堆化和自底向上的堆化。

以自底向上的堆化过程为例：

先计算出最后一个非叶子节点的索引 lastNonLeaf 。在一个堆中，最后一个非叶子节点的索引可以通过 (n-2) / 2 计算得到，其中 n 是堆中元素的个数。

然后从最后一个非叶子节点 lastNonLeaf 开始，逐个向前遍历所有的非叶子节点，对每个节点执行自底向上的堆化操作。

class MaxHeap {
  // ...（之前的代码）

  buildHeap(arr) {
    this.heap = arr;
    const lastNonLeaf = Math.floor((this.heap.length - 2) / 2);

    for (let i = lastNonLeaf; i >= 0; i--) {
      this._heapifyDown(i);
    }
  }
}

// Example usage
const maxHeap = new MaxHeap();
maxHeap.buildHeap([8, 4, 10, 3, 5]);
console.log(maxHeap.heap); // Output: [10, 5, 8, 3, 4]

堆的应用

堆作为一种数据结构，有着广泛的应用，其中包括但不限于以下情景：

堆排序：基于堆实现的一种排序算法。
优先队列：基于堆实现的一种数据结构，能够快速访问最大（或最小）值。
Dijkstra 算法：用于计算最短路径的图算法中使用了优先队列，通常基于堆实现。
操作系统调度：一些操作系统中使用堆来管理进程或任务的优先级。

堆排序

堆排序是一种基于堆的排序算法，它利用堆的性质进行排序。堆排序分为两个阶段：建堆和排序。

1. 建堆

在建堆阶段，将数组视为一个完全二叉树，然后从最后一个非叶子节点开始，依次对每个节点进行堆化操作，使得整个数组满足堆的性质。

function buildHeap(arr) {
  const lastNonLeaf = Math.floor((arr.length - 2) / 2);

  for (let i = lastNonLeaf; i >= 0; i--) {
    heapifyDown(arr, i, arr.length);
  }
}

// Example usage
const arrayToSort = [8, 4, 10, 3, 5];
buildHeap(arrayToSort);
console.log(arrayToSort); // Output: [10, 5, 8, 3, 4]

2. 排序

在建堆完成后，最大（或最小）元素已经位于堆的根节点。

以大顶堆为例，数组中的第一个元素就是堆顶，也就是最大的元素。把它跟最后一个元素交换，那最大元素就放到了下标为 n 的位置。

这个过程有点类似上面讲的“删除堆顶元素”的操作，当堆顶元素移除之后，把下标为 n 的元素放到堆顶，然后再通过堆化的方法，将剩下的 n-1 个元素重新构建成堆。堆化完成之后，再取堆顶的元素，放到下标是 n-1 的位置，一直重复这个过程，直到最后堆中只剩下标为 1 的一个元素，排序工作就完成了。

function heapSort(arr) {
  buildHeap(arr);

  for (let i = arr.length - 1; i > 0; i--) {
    [arr[0], arr[i]] = [arr[i], arr[0]];
    heapifyDown(arr, 0, i);
  }
}

// Example usage
const arrayToSort = [8, 4, 10, 3, 5];
heapSort(arrayToSort);
console.log(arrayToSort); // Output: [3, 4, 5, 8, 10]

堆排序包括建堆和排序两个操作，建堆过程的时间复杂度是 O(n) ，排序过程的时间复杂度是 O(nlog n) ，所以，堆排序整体的时间复杂度是 O(nlog n) 。

优先队列

优先队列是一种支持按优先级顺序访问元素的数据结构。基于堆实现的优先队列可以在 O(log n) 的时间内找到并删除具有最高（或最低）优先级的元素。

class PriorityQueue {
  constructor() {
    this.heap = [];
  }

  enqueue(item) {
    this.heap.push(item);
    this._heapifyUp();
  }

  dequeue() {
    if (this.heap.length === 0) {
      return null;
    }

    const highestPriority = this.heap[0];
    const last = this.heap.pop();

    if (this.heap.length > 0) {
      this.heap[0] = last;
      this._heapifyDown(0);
    }

    return highestPriority;
  }

  _heapifyUp() {
    // Similar to the previous MaxHeap example
    // ...
  }

  _heapifyDown(index) {
    // Similar to the previous MaxHeap example
    // ...
  }
}

// Example usage
const priorityQueue = new PriorityQueue();
priorityQueue.enqueue({ value: "Task A", priority: 2 });
priorityQueue.enqueue({ value: "Task B", priority: 1 });
priorityQueue.enqueue({ value: "Task C", priority: 3 });

console.log(priorityQueue.dequeue()); // Output: { value: "Task C", priority: 3 }
console.log(priorityQueue.dequeue()); // Output: { value: "Task A", priority: 2 }

TOP K 问题

求 Top K 问题分为两类：一类是针对静态数据集合，数据集合事先确定，不会再变；另一类是针对动态数据集合，数据集合事先并不确定，有数据动态地加入到集合中。

静态数组

针对静态数据，想要在一个包含 n 个数据的数组中，查找前 K 大的数据，可以维护一个大小为 K 的小顶堆：

顺序遍历数组，从数组中取出取数据与堆顶元素比较；
如果比堆顶元素大，就把堆顶元素删除，并且将这个元素插入到堆中；
如果比堆顶元素小，则不做处理，继续遍历数组；
遍历完数组中的数据之后，堆中的数据就是前 K 大数据；

遍历数组需要 O(n) 的时间复杂度，一次堆化操作需要 O(logK) 的时间复杂度，所以最坏情况下，n 个元素都入堆一次，所以时间复杂度就是 O(nlogK) 。

动态数组

针对动态数据求得 Top K 就是实时 Top K。

假设数组在不断插入数据，如果每次求前 K 大的数据，都基于当前的数据重新计算的话，那时间复杂度就是 O(nlogK)，n 表示当前的数据的大小。

实际上，可以维护一个 K 大小的小顶堆，当有数据被添加到数组中时，就拿它与堆顶的元素对比。

如果比堆顶元素大，就把堆顶元素删除，并且将这个元素插入到堆中；
如果比堆顶元素小，则不做处理；

这样，无论任何时候需要查询当前的前 K 大的数据，都可以立刻返回。

对于插入操作，最坏情况下，我们需要进行堆化的次数是堆的高度，即 log K。因此，插入操作的时间复杂度是 O(log K)。在初始化时，需要将前 K 个元素构建最小堆，这一过程的时间复杂度是 O(Klog K)。总体来说，时间复杂度主要受插入操作的影响，为 O(log K)。

📌 703. 数据流中的第 K 大元素 - LeetCodeopen in new window

💻 题目大意

设计一个找到数据流中第 k 大元素的类（class）。注意是排序后的第 k 大元素，不是第 k 个不同的元素。

请实现 KthLargest 类：

KthLargest(int k, int[] nums) 使用整数 k 和整数流 nums 初始化对象。
int add(int val) 将 val 插入数据流 nums 后，返回当前数据流中第 k 大的元素

💡 解题思路

动态数组求 Top K 问题，使用大小为 K 的小顶堆。

💎 代码

class KthLargest {
  // @param {number} k
  // @param {number[]} nums
  constructor(k, nums) {
    this.k = k;
    this.heap = [];
    for (let i of nums) {
      this.add(i);
    }
  }
  // @param {number} val
  // @return {number}
  add(val) {
    if (this.heap.length < this.k) {
      this.heap.push(val);
      this.heapifyUp(this.heap.length - 1);
    } else if (this.heap[0] < val) {
      this.heap[0] = val;
      this.heapifyDown(0);
    }
    return this.heap[0];
  }

  heapifyUp(index) {
    while (index > 0) {
      const parent = Math.floor((index - 1) / 2);
      if (this.heap[parent] > this.heap[index]) {
        [this.heap[parent], this.heap[index]] = [
          this.heap[index],
          this.heap[parent],
        ];
        index = parent;
      } else {
        break;
      }
    }
  }

  heapifyDown(index) {
    const left = 2 * index + 1;
    const right = 2 * index + 2;
    let min = index;

    if (left < this.heap.length && this.heap[left] < this.heap[min]) {
      min = left;
    }
    if (right < this.heap.length && this.heap[right] < this.heap[min]) {
      min = right;
    }
    if (min !== index) {
      [this.heap[min], this.heap[index]] = [this.heap[index], this.heap[min]];
      this.heapifyDown(min);
    }
  }
}

#### 📌 [703. 数据流中的第 K 大元素 - LeetCode](https://leetcode.com/problems/kth-largest-element-in-a-stream/)

#### 💻 **题目大意**

设计一个找到数据流中第 `k` 大元素的类（class）。注意是排序后的第 `k` 大元素，不是第 `k` 个不同的元素。

请实现 `KthLargest` 类：

- `KthLargest(int k, int[] nums)` 使用整数 `k` 和整数流 `nums` 初始化对象。
- `int add(int val)` 将 `val` 插入数据流 `nums` 后，返回当前数据流中第 `k` 大的元素

#### 💡 **解题思路**

动态数组求 Top K 问题，使用大小为 K 的小顶堆。

#### 💎 **代码**

```javascript
class KthLargest {
  // @param {number} k
  // @param {number[]} nums
  constructor(k, nums) {
    this.k = k;
    this.heap = [];
    for (let i of nums) {
      this.add(i);
    }
  }
  // @param {number} val
  // @return {number}
  add(val) {
    if (this.heap.length < this.k) {
      this.heap.push(val);
      this.heapifyUp(this.heap.length - 1);
    } else if (this.heap[0] < val) {
      this.heap[0] = val;
      this.heapifyDown(0);
    }
    return this.heap[0];
  }

  heapifyUp(index) {
    while (index > 0) {
      const parent = Math.floor((index - 1) / 2);
      if (this.heap[parent] > this.heap[index]) {
        [this.heap[parent], this.heap[index]] = [
          this.heap[index],
          this.heap[parent],
        ];
        index = parent;
      } else {
        break;
      }
    }
  }

  heapifyDown(index) {
    const left = 2 * index + 1;
    const right = 2 * index + 2;
    let min = index;

    if (left < this.heap.length && this.heap[left] < this.heap[min]) {
      min = left;
    }
    if (right < this.heap.length && this.heap[right] < this.heap[min]) {
      min = right;
    }
    if (min !== index) {
      [this.heap[min], this.heap[index]] = [this.heap[index], this.heap[min]];
      this.heapifyDown(min);
    }
  }
}
```

求中位数

Dijkstra 算法

Dijkstra 算法是一种用于计算图中最短路径的贪心算法。在算法的实现中，使用了基于最小堆的优先队列来高效地选择下一个要探索的节点。

function dijkstra(graph, start) {
  const distances = {};
  const priorityQueue = new PriorityQueue();

  // Initialize distances and enqueue the start node
  for (const vertex in graph) {
    distances[vertex] = Infinity;
  }
  distances[start] = 0;
  priorityQueue.enqueue({ node: start, distance: 0 });

  while (priorityQueue.heap.length > 0) {
    const { node, distance } = priorityQueue.dequeue();

    if (distance > distances[node]) {
      continue;
    }

    for (const neighbor in graph[node]) {
      const newDistance = distance + graph[node][neighbor];
      if (newDistance < distances[neighbor]) {
        distances[neighbor] = newDistance;
        priorityQueue.enqueue({ node: neighbor, distance: newDistance });
      }
    }
  }

  return distances;
}

// Example usage
const weightedGraph = {
  A: { B: 1, C: 4 },
  B: { A: 1, C: 2, D: 5 },
  C: { A: 4, B: 2, D: 1 },
  D: { B: 5, C: 1 },
};

console.log(dijkstra(weightedGraph, "A"));
// Output: { A: 0, B: 1, C: 3, D: 4 }

操作系统调度

在操作系统中，任务调度是一个重要的问题。通过使用基于堆的数据结构，可以轻松地管理和调度任务的优先级。

2.7 堆

# 2.7 堆

# 堆的定义

# 堆的实现

# 1. 插入操作

# 2. 删除操作

# 3. 堆化操作

# 堆的应用

# 堆排序

# 1. 建堆

# 2. 排序

# 优先队列

# TOP K 问题

# 静态数组

# 动态数组

# 📌 703. 数据流中的第 K 大元素 - LeetCodeopen in new window

# 💻 题目大意

# 💡 解题思路

# 💎 代码

# 求中位数

# Dijkstra 算法

# 操作系统调度

2.7 堆

堆的定义

堆的实现

1. 插入操作

2. 删除操作

3. 堆化操作

堆的应用

堆排序

1. 建堆

2. 排序

优先队列

TOP K 问题

静态数组

动态数组

📌 703. 数据流中的第 K 大元素 - LeetCodeopen in new window

💻 题目大意

💡 解题思路

💎 代码

求中位数

Dijkstra 算法

操作系统调度